Efekt Dzhanibekova
Dziś coś z fizyki dla dociekliwych: The Efekt Dzhanibekova, znane również jako twierdzenie o rakietach tenisowych, wyjaśnia niestabilność wirujących ciał z trzema różnymi momentami bezwładności. Moment bezwładności wskazuje na odporność ciała na zmiany jego ruchu obrotowego. Zależy to od konkretnej osi obrotu i geometrii. Zrozumienie dynamiki klasycznych systemów hamiltonowskich jest nadal kluczowym celem z wieloma zastosowaniami, które wykraczają daleko poza ich opis matematyczny. W przypadku systemów integrowalnych z kilkoma stopniami swobody, efektywne podejście opiera się na analizie geometrycznej, aby scharakteryzować właściwości dynamiczne układu mechanicznego. Takie zjawiska geometryczne są zazwyczaj źródłem trwałości pewnych efektów, które można zaobserwować eksperymentalnie. jednym z nich jest tzw Efekt Dzhanibekova lub nazywany również efektem rakiety tenisowej.
Efekt Dschanibekowa w nieważkości ISS
Doskonałe i szczegółowe teoretyczne wyprowadzenie tego zjawiska można znaleźć tutaj (https://arxiv.org/pdf/1606.08237.pdf). Mamy tutaj do czynienia z osobą nieco ostrzejszą, ale która mimo wszystko wyjaśnia to zjawisko. Niestety, potrzebna jest tutaj pewna wcześniejsza znajomość dynamiki ciał sztywnych:
Rozważmy macierz bezwładności (przekątną) z momentami bezwładności I1 i I2 i I3 taką, że I1 jest najmniejsze, a I3 jest największe. Rozważmy teraz ruch wokół osi głównego momentu bezwładności I3. Wektor prędkości kątowej to:
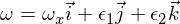
gdzie epsilony są małymi zaburzeniami w pozostałych dwóch głównych osiach. Jeśli teraz wstawisz to do równań Eulera, otrzymasz:
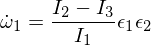
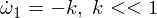
Teraz różniczkujemy drugie równanie Eulera:
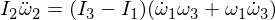
Zastąpienie omega 1 i omega 3 w naszym wyrażeniu, a ponieważ pomnożenie epsilonów sprawia, że są one na tyle małe, że można je zignorować,
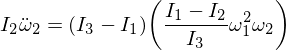
To daje nam równanie różniczkowe dla Omega 2 w postaci:
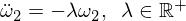
Podstawowe rozwiązanie to:
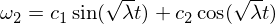
Stąd wiemy, że zaburzenie rotacyjne w osi omega-1 jest stabilne i powoduje okresowe ruchy, czyli w terminologii sztywnego ruchu ciała, że dokonuje precesji. Zaburzenie omega 3 wynika z podobnego argumentu, jak powyżej, i zostawię to jako ćwiczenie, abyś mógł przez to przejść. Dla osi pośredniej mamy:
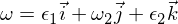
Wstawione do równań Eulera:
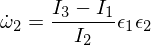
Różniczkowanie trzeciego równania Eulera daje:
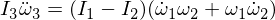
Zastąpmy nasze wyrażenia pochodne:
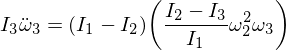
Teraz zmień układ i wyprowadź następujące równanie różniczkowe:
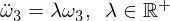
Zauważ, że współczynnik jest teraz dodatni, co w związku z tym prowadzi do rozwiązań wykładniczych:
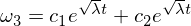
To rozwiązanie pokazuje, że omega 3 jest niestabilny z zaburzeniem kwasów omega 2 wzdłuż osi pośredniej!
Co to oznacza?
Teraz możemy połączyć wszystko, co wyprowadziliśmy i nauczyliśmy się rozumieć twierdzenie. Mówiąc prościej, jeśli obrót wzdłuż osi pośredniej zostanie zakłócony, otrzymamy równanie różniczkowe z rozwiązaniami wykładniczymi. Prowadzi to do niestabilnego ruchu, w przeciwieństwie do precyzyjnego ruchu obserwowanego w pozostałych dwóch osiach. Ten wynik jest dość zaskakujący. Nie ma intuicyjnego poparcia dla takiego twierdzenia, ponieważ nie możemy sobie wyobrazić, dlaczego pośredni moment bezwładności miałby spowodować niestabilny obrót. Wygląda na to, że ma to charakter czysto matematyczny.