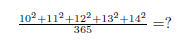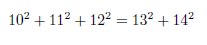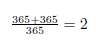Sekrety algebry

Ostatni artykuł miał miłą odpowiedź (dzięki za to). A więc dzisiaj coś ze świata „zapomnianej matematyki” - baw się dobrze!

Arytmetyka często nie jest w stanie udowodnić niektórych jej twierdz za pomocą niejasnych środków. W takich przypadkach potrzebujemy bardziej ogólnych metod algebry. W przypadku tego typu twierdzenia arytmetycznego, które jest uzasadnione algebraicznie, istnieje wiele reguł dotyczących skróconych operacji arytmetycznych.

Mnożenie prędkości:

W dawnych czasach, bez komputerów i kalkulatorów, wielcy arytmetyki stosowali wiele prostych sztuczek algebraicznych; aby ułatwić Ci życie:

„X” oznacza mnożenie (byliśmy zbyt leniwi, aby wypróbować LaTeX :-))

Spójrzmy na:

988² =?

Czy potrafisz rozwiązać to w swojej głowie?

To bardzo proste, przyjrzyjmy się bliżej:

988 x 988 = (988 + 12) x (998-12) + 12² = 1000 x 976 + 144 = 976 144

Łatwo też zrozumieć, co się tutaj dzieje:

(a + b) (a - b) + b² = a² - b² + b² = a²

Jak dotąd OK, tak dobrze. Teraz spróbujmy szybko policzyć - nawet kombinacje, takie jak

986 x 997, bez kalkulatora!

986 x 997 = (986 - 3) x 1000 + 3 x 14 = 983

Co tu się stało? Możemy zapisać czynniki w następujący sposób:

Czytaj więcej

„Trudny” problem

Dziś coś z kategorii „zapomniana matematyka”. Zawsze istnieją bardzo interesujące algebraiczne zależności liczbowe, które niestety są rzadkie lub wcale nie występują w programie nauczania, ale które poszerzają zrozumienie liczb i intuicję matematyczną.

Powiedzmy, że ktoś prosi Cię o rozwiązanie następnego równania bez żadnych narzędzi technicznych.

Potrafisz to zrobić?

Ok na pierwszy rzut oka nie jest takie proste. Ale kiedy znasz specjalną i interesującą zależność między tymi liczbami, jest to naprawdę proste:

Lewe składniki równania to: 100 + 121 + 144 = 365; Innymi słowy:

Ok, użyjmy prostej algebry, aby dowiedzieć się, czy możemy znaleźć więcej takich sekwencji: Pierwsza liczba, której szukamy, to "x":